信息论与熵

特征编码

直接编码

e.g.
1. 性别\(S\)：{男，女}——\(\{0，1\}\)
2. 归属地\(L\):{亚洲，欧洲，非洲，美洲}——\(\{0,1,2,3\}\)
3. 浏览器工具\(B\):{Chrome,IE,360,Firefox,Safari}——\(\{0,1,2,3,4\}\)
“来自【欧洲】，使用【Firefox】的【男性】”表示为\([0,1,3]\)。

One-hot 编码

e.g.
1. 性别\(S\)：{男，女}——\(\{01，10\}\)
2. 归属地\(L\):{亚洲，欧洲，非洲，美洲}——\(\{0001,0010,0100,1000\}\)
3. 浏览器工具\(B\):{Chrome,IE,360,Firefox,Safari}——\(\{00001,00010,00100,01000,10000\}\)
“来自【欧洲】，使用【Firefox】的【男性】”表示为 {01,00,0000,0010,0000,0000,00000,00000,00000,01000,00000}, 可简写为{1,0,0,1,0,0,0,0,0,1,0}

Dummy编码(哑变量编码、虚拟变量编码)

将One-hot编码第一位去掉

压缩编码

聚类

定义：将样本数据集\(D\)划分成\(k\)个互不相交的子集 ### 特征降维
优点：

维度灾难：随着特征数量的增加，数据在高维空间中变得稀疏，导致模型难以学习有效的模式。
计算效率：高维数据会显著增加计算和存储成本。
噪声和冗余：某些特征可能是冗余的或包含噪声，降维可以去除这些无用的信息。
可视化：将高维数据降到2D或3D，便于可视化分析。

特性：

纠错输出码(ECEO)

示例图片 - 编码：对\(N(左图为4)\)个类进行\(M\)次划分，产生\(M(左图为5)\)个分类器(\(f\)) - 解码： \(M\) 个分类器对测试样本进行预测，得到 \(M\) 个预测标记，将其组成编码；这个编码与 N 个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测的结果。

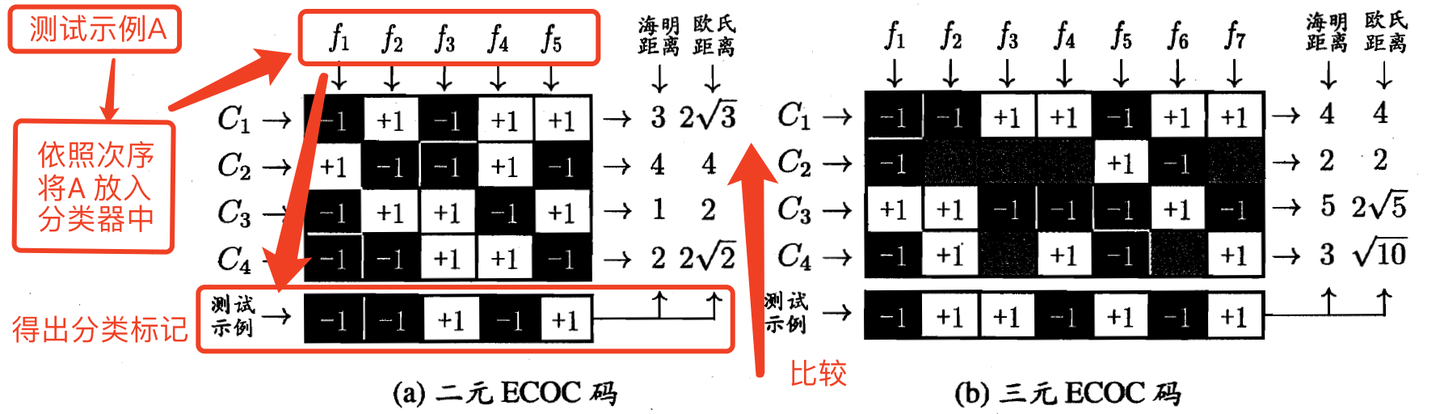
聚类

聚类方法：预测样本选择为与某一类的聚类中心的距离最小的类别。（最相似） ## 自编码

欠完备自编码
- 最小化\(L(x,decoder(encoder(x)))\)
稀疏自编码当隐藏编码\(h\)维数大于输入样本\(x\)维数时，即使是表达能力稍差的线性编、解码器，样本复制风险也会增强，这类自编码器被称为过完备自编码器。
- 最小化\(L(x,decoder(encoder(x)))+R(encoder(x))\) 其中\(R(encoder(\boldsymbol{x}))\)称作归纳偏好，用于产生稀疏解。一般取\(h\)的\(p-范数\) L-p范数： \[L_p=||\boldsymbol{x}||_p=\sqrt[p]{\sum_{i=1}^{n}|x_i|^p }\]
收缩自编码器引入一个与输入样本相关的正则项，迫使自编码器学习训练数据分布特性。
- e.g. 定义正则化项\(R(f(x),x)=\lambda \sum_{i=1}^{d'} ||\nabla_xf(x)||_2^2\) ,其中\(||\nabla_xf(x)||_2^2\)为\(f(x)\)沿\(x\)方向梯度向量2-范数的平方，则目标为\(\text{arg min}_{encoder,decoder}(L(x,decoder(encoder(x)))+R(encoder(x),x))\)

不确定性与熵

定义与性质

与事件发生概率负相关
同时发生时，信息量可加给定信离散型随机变量\(X\)，其在\(X=x_i\)处提供的信息量定义为 \[ h(X=x_i)=-log_af(x_i) \] \(f(x_i)\)为随机变量\(X\)取值为\(x_i\)的概率分布 信息熵： \[ Ent(X)=-\sum_{i=1}^n f(x_i)log_a(f(x_i))(离散型) \] \[ Ent(X)=-\int_{-\infty}^{+\infty} f(x)log_a(f(x))(连续型) \]

联合熵

离散型： \[ \text{Ent}(X,Y) = - \sum_{i = 1}^{n} \sum_{j = 1}^{m} f(x_i, y_j) \log_a (f(x_i, y_j)) \]
连续型： \[ \text{Ent}(X,Y)=-\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)\log_a(f(x,y))\mathrm{d}x\mathrm{d}y \]
性质
1. 非负性
2. 联合熵大于各独立熵
3. 联合熵小于所有独立熵的和 ### 条件熵
离散型： \[ \text{Ent}(Y\mid X = x_i)=-\sum_{j = 1}^{m} f(y_j\mid x_i)\log_a(f(y_j\mid x_i)) \] 其中, \(f(y_{j} | x_{i})\) 为随机变量 X 取值为 \(x_{i}\) 时随机变量 Y 的概率分布列。数学期望： \[\begin{aligned} Ent(Y | X) & =-\sum_{i=1}^{n} f\left(x_{i}\right) \sum_{j=1}^{m} f\left(y_{j} | x_{i}\right) log _{a}\left(f\left(y_{j} | x_{i}\right)\right) \\ & =-\sum_{i=1}^{n} \sum_{j=1}^{m} f\left(x_{i}, y_{j}\right) log _{a}\left(f\left(y_{j} | x_{i}\right)\right) \end{aligned}\] 其中, \(f(x_{i})\) 为随机变量 X 的概率分布列; \(f(x_{i}, y_{j})\) 为随机变量 X 与 Y 的联合概率分布列。
连续型：\[Ent\left(Y | X=x_{i}\right)=-\int_{-\infty}^{+\infty} f\left(y | x_{i}\right) log _{a}\left(f\left(y | x_{i}\right)\right) dy\] 其中, \(f(y | x_{i})\) 为随机变量 X 取值为 \(x_{i}\) 时随机变量 Y 的概率密度函数数学期望： \[\begin{aligned} Ent(Y | X) & =-\int_{-\infty}^{+\infty} f(x) \sum_{j=1}^{m} f\left(y_{j} | x\right) log _{a}\left(f\left(y_{j} | x\right)\right) d x \\ & =-\int_{-\infty}^{+\infty} \sum_{j=1}^{m} f\left(x, y_{j}\right) log _{a}\left(f\left(y_{j} | x\right)\right) dx \end{aligned}\] 其中, \(f(x)\) 为随机变量 X 的概率密度函数; \(f(y_{j} | x)\) 为随机变量 \(X\) 取值为\(x\)时随机变量 \(Y\) 的概率分布列; \(f(x, y_{j})\) 为随机变量 \(Y\) 的所有取值对应的随机变量 \(X\) 的概率密度函数。 ### 交叉熵与损失熵

假设连续型随机变量 X 的两个分布的概率密度函数分别为 \(f_{0}(x)\) 和 \(f_{1}(x)\) ,其中, \(f_{0}(x)\) 为真实分布, \(f_{1}(x)\) 为估计到的非真实分布,则二者的交叉嫡定义为 \[Ent\left(f_{0}, f_{1}\right)=-\int_{-\infty}^{+\infty} f_{0}(x) log _{a} f_{1}(x) d x\] 其中\(f_{0}(x) \in[0 \to 1]\) 、 \(f_{1}(x) \in[0→1]\)且 \[\begin{aligned} Ent\left(f_{0}\right)-Ent\left(f_{0}, f_{1}\right) & \leq \int_{-\infty}^{+\infty} f_{0}(x)\left(\frac{f_{1}(x)}{f_{0}(x)}-1\right) d x ——(log_ax\leq x-1)\\ & =\int_{-\infty}^{+\infty}\left(f_{1}(x)-f_{0}(x)\right) d x \\ & =\int_{-\infty}^{+\infty} f_{1}(x) d x-\int_{-\infty}^{+\infty} f_{0}(x) d x=0 \end{aligned}\] 即\(Ent(f_{0}) ≤Ent(f_{0}, f_{1})\) 恒成立（吉布斯不等式）,当且仅当 \(f_{0}= f_{1}\) 时等号成立。

相对熵与KL散度

实际上,前文吉布斯不等式推导式的左端定义了连续随机变量 X 的两个概率分布的相对嫡,也称作KL散度(Kullback-Leible Diverence),即 \[\begin{aligned} D_{KL}\left(f_{0} \| f_{1}\right) & =-\int_{-\infty}^{+\infty} f_{0}(x) log _{a}\left(\frac{f_{1}(x)}{f_{0}(x)}\right) d x \\ & =\int_{-\infty}^{+\infty} f_{0}(x) log _{a}\left(\frac{f_{0}(x)}{f_{1}(x)}\right) d x \\ & =Ent\left(f_{0}, f_{1}\right)-Ent\left(f_{0}\right) \end{aligned}\] 显然, \(D_{KL}(f_{0} \| f_{1})=Ent(f_{0}, f_{1})-Ent(f_{0})\) 且 \(D_{KL}(f_{0} \| f_{1}) ≥0\) 。另外,不难证明,除非\(f_{0}=f_{1}\) ,否则 \(D_{KL}(f_{0} \| f_{1}) ≠D_{KL}(f_{1} \| f_{0})\) 。 ## 互信息

定义

若已完整学到 X 的所有知识,则对 Y 知识的认知理解增量为 \(I(Y ; X)\) 若随机变量 X 与 Y 均为连续型变量,则形式化地 \[\begin{aligned} I(Y, X)= & Ent(Y)-Ent(Y | X) \\ & =-\int_{-\infty}^{+\infty} f(y) log _{a}(f(y)) d y+\int_{-\infty}^{+\infty} f(x) Ent(Y | x) d x \\ & =-\int_{-\infty}^{+\infty}\left(\int_{-\infty}^{+\infty} f(x, y) d x\right) log _{a}(f(y)) d y+ \\ & \int_{-\infty}^{+\infty} f(x) \int_{-\infty}^{+\infty} f(y | x) log _{a}(f(y | x)) d y d x \\ & =-\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) log _{a}(f(y)) d x d y+\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) log _{a}\left(\frac{f(x, y)}{f(x)}\right) d x d y \\ = & \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) log _{a}\left(\frac{f(x, y)}{f(x) f(y)}\right) d x d y \end{aligned}\] 其中, \(f(x)\) 与 \(f(y)\) 分别为随机变量 X 与 Y 的概率密度函数; \(f(x, y)\) 为随机变量 X 与 Y 的联合概率密度函数; \(f(y | x)\) 为条件概率密度函数。 - 互信息定义的交叉嫡形式: \(I(Y ; X)=D_{KL}(f(x, y) \| f(x) f(y))\) 。